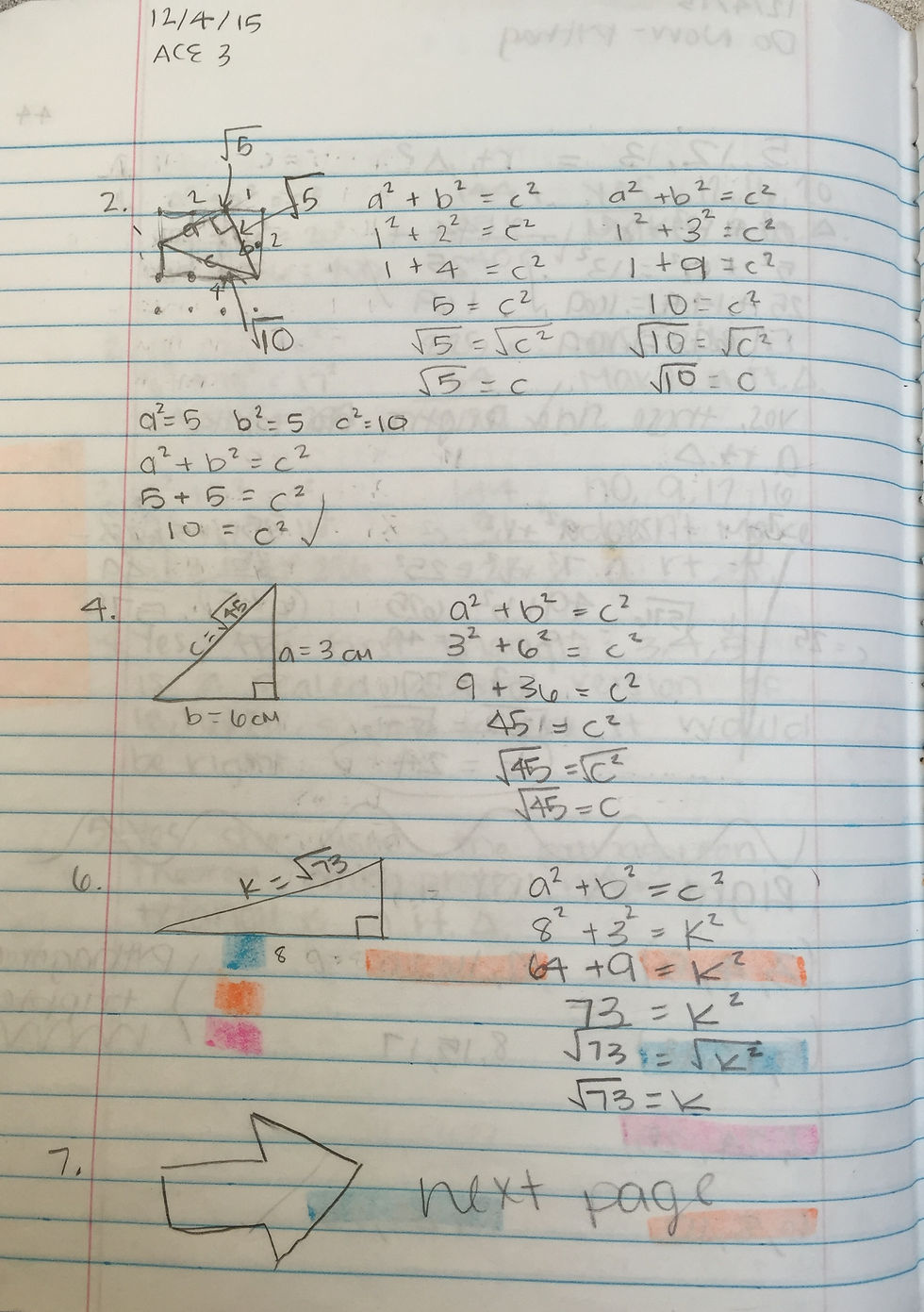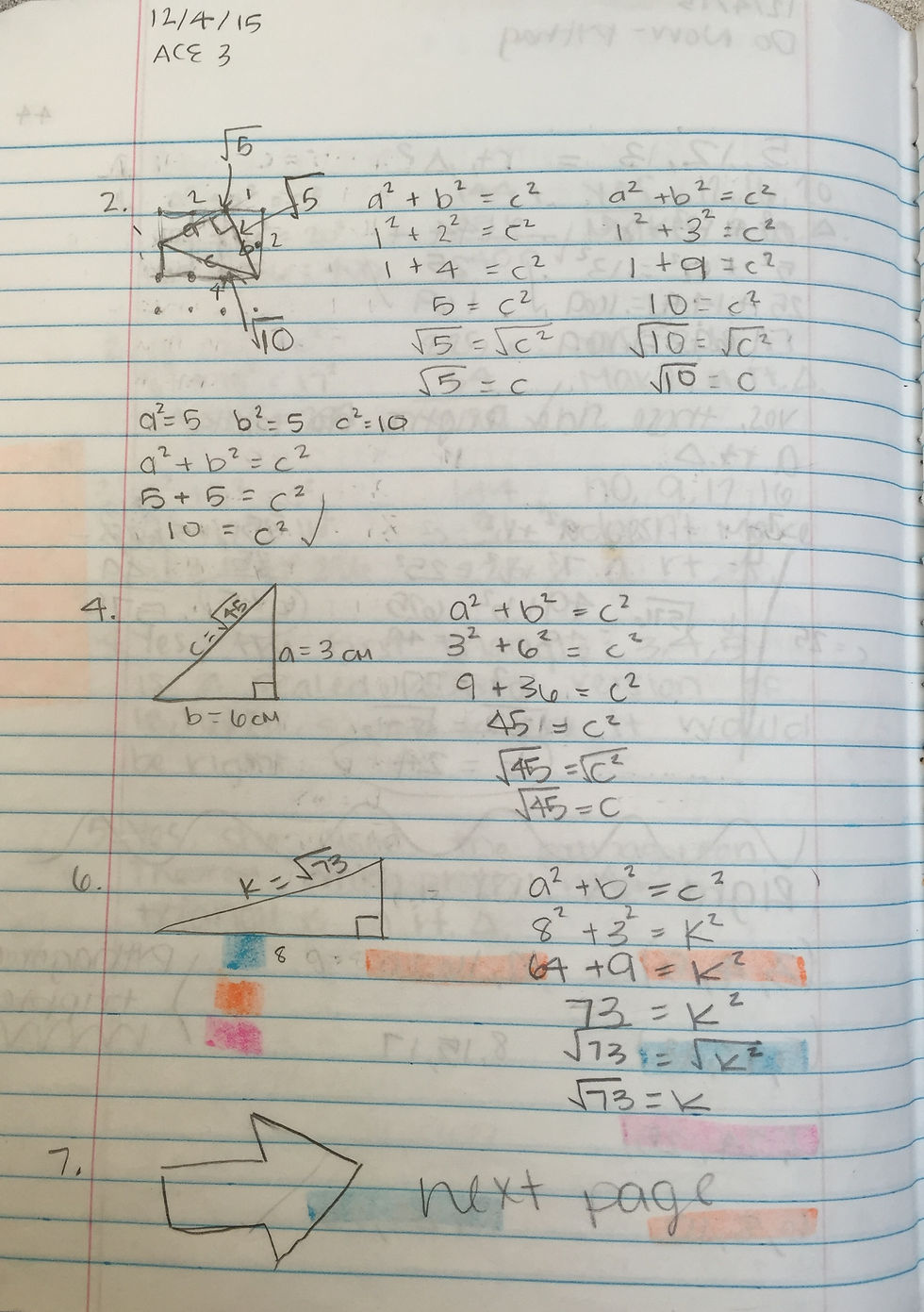We write reflections to explain exactly how our skills and knowledge have grown and developed throughout the year. It is also to make me look back and think about how much I’ve learned, and to think ahead about how it is going to help me in the future. So far this year, math has been a challenge. Last year math was really hard because I didn’t connect with the way my teacher taught. Because of this I had a lot of anxiety coming into math this year. My only problem is that the content is really new and different, and I was not very used to even learning in math class, so that’s a bit of a challenge this year, but it’s worth it. Math can be very confusing and hard to understand sometimes so it is really important to know how to write it maturely. When we write math correctly so that it would make sense to a mathematician, it would make sense to our teachers and our peers. Dr. Schaefer, my math teacher this year, has really tried to get it through to us how important showing work—and correct work is. So for the first semester of eighth grade I have really grown in showing mature work to support any math problems I solve.

As it says above, this year in math I have developed better skills in writing complete work. I have learned how to make sure what I am writing down displays exactly how I solved the problem, my thought process, and the steps I took to reach my answer. I should note that before eighth grade started, I would only show work by writing out some random numbers, but it wouldn’t make logical sense, nothing actually significant. I had never even thought that I wasn’t making sense in my work. My teacher then told me how to look at things as if I was a mathematician. When I looked at my work, I noticed that it didn’t have any context and it didn’t seem right. So I really paid attention when Dr. Schaefer told us how we should write out real work, it taught me a lot and it inspired my growth.

One of the first things we did with the actual Pythagorean Theorem was take notes and do some practice problems. The Pythagorean Theorem is a principle in math that says in a right triangle, a^2+b^2=c^2. A right triangle is a triangle with one 90-degree angle and two other acute angles. And a, b, and c being three side lengths in the triangle. A and b represent the legs of the triangle, the two sides that make the right angle at their vertex (the point where they meet). Side c is the hypotenuse, or the side that is across from the right angle, is always the longest side in a right triangle. You can see in my work I just have random letters equaling numbers for both problems on this page. I knew what I meant and where I got everything but no one else would. You can see that I don’t really understand how to communicate mathematically here. In my next example you can see how that changes.

The next artifact is an example of some ACE problems we did using the Pythagorean Theorem. ACE stands for the following: A, applications which applies your simple knowledge of the skills (easy difficulty). C, connections which is where you need to think harder to make connections between the skills you are learning and some learned previously (medium difficulty). E, extensions which are made to help you extend your math skills and think further into things you haven’t learned yet (hard difficulty). The three different levels are meant to challenge you and provide for the best learning possible. These problems were completed shortly after we learned how to correctly represent our work. I took extra time to make sure I wrote everything out correctly and I included every element of work I was supposed to. You can see in the paper where I made it clear what I was doing and it’s easy to read my work. On question two, I had three different sets of work to find three different side lengths of the triangle and they are all clearly set apart and you can tell which is which. As well you can see exactly how I solved each problem and how I was thinking to get me to my answer. That shows a lot of growth between the two papers attached.

In conclusion, I think writing out sophisticated, mature work when answering math problems is a great skill to have and I know I have grown a lot in doing that over the course of my eighth grade year. In my future at STEM, mature work is going to help me score higher on tests and understand the problems more clearly. Communicating Math clearly is also important because it can then be read and critiqued by peers and the teacher which is very good. The “M” in “STEM” stands for Mathematics, so it’s easy to tell that our school really values math. For me, any improvements in any of the STEM subjects are great improvements, which means this one is too. I am very glad I have gained this skill. It will allow me to excel in my future as not only a STEM student, but in college, jobs, and life.